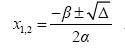Κλήση συνάρτησης από συνάρτηση - συμβολοσειρά και λίστα

Να γράψετε μια συνάρτηση σε Python η οποία θα δέχεται μια λέξη σε κεφαλαία και ελληνικά και θα επιστρέφει το πλήθος των φωνηέντων που έχει. Στη συνέχεια, να γράψετε μια δεύτερη συνάρτηση, η οποία θα δέχεται μια λίστα από λέξεις σε κεφαλαία και ελληνικά και θα επιστρέφει τη λέξη με τα περισσότερα φωνήεντα.

 

 

 

 Ενδεικτική απάντηση με κυρίως πρόγραμμα - παράδειγμα εφαρμογής

Επίλυση δευτεροβάθμιας εξίσωσης με html/javascript

Επίλυση δευτεροβάθμιας εξίσωσης αx²+βx+γ=0

Συντελεστής α:

Συντελεστής β:

Συντελεστής γ:

Διακρίνουσα :

x1:

x2:

Το αρχείο html/javascript για λήψη

Επίλυση εξίσωσης δευτέρου βαθμού με συνάρτηση της Python 2.7

 Επίλυση εξίσωσης δευτέρου βαθμού της μορφής αx² + βx + γ = 0, με α ≠ 0

με τη χρήση της διακρίνουσας Δ με Python 2.7

Δ = β2 – 4αγ	Η εξίσωση αx2 + βx + γ = 0, α ≠ 0
Δ > 0	Έχει δύο ρίζες άνισες τις
Δ = 0	Έχει μια διπλή ρίζα τη
Δ < 0	Είναι αδύνατη στο R .

Πηγή: 

http://users.sch.gr/fergadioti1/Institude_Geogebra/applets/A_alg_3exisoseis/33.html

Στην Python δημιουργούμε μία συνάρτηση quad(a,b,c) με παραμέτρους τους συντελεστές της δευτεροβάθμιας εξίσωσης α,β και γ (a,b,c).

Πρώτα υπολογίζουμε την διακρίνουσα  Δ = β² – 4αγ    (d=b**2-4*a*c)

Aν d<0 επιστρέφει το d και τα μηνύματα: "No real solution",  "No real solution"

Αλλιώς αν το d>0 η συνάρτηση επιστρέφει το d και δύο ρίζες:

x1=(-b+math.sqrt(d))/(2*a)

x2=(-b-math.sqrt(d))/(2*a)

return d,x1,x2

Τέλος αν d=0 (d==0)  η συνάρτηση επιστρέφει το d και μία διπλή ρίζα:

 x=-b/float(2*a)

return d,x,x

 

Η συνάρτηση και οι κλήσεις της συνάρτησης από τη γραμμή εντολών (εκτέλεση)

 Το αρχείο Python με τη συνάρτηση επίλυσης δευτεροβάθμιας εξίσωσης

Συνάρτηση δημιουργίας λίστας της ακολουθίας Fibonacci με Python

 

Οι Αριθμοί Φιμπονάτσι είναι οι αριθμοί της παρακάτω ακέραιας ακολουθίας:

 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , … 

Εξ ορισμού, οι πρώτοι δύο αριθμοί Φιμπονάτσι είναι το 0 και το 1, και κάθε επόμενος αριθμός είναι το άθροισμα των δύο προηγούμενων.

Σε μαθηματικούς όρους, η ακολουθία Fn των αριθμών Φιμπονάτσι ορίζεται από τον αναδρομικό τύπο: 

F n = F n − 1 + F n − 2  

με F 0 = 0 και F 1 = 1 

Πηγή: https://el.wikipedia.org/wiki/Ακολουθία_Φιμπονάτσι

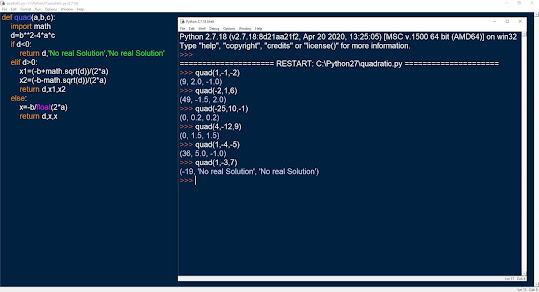
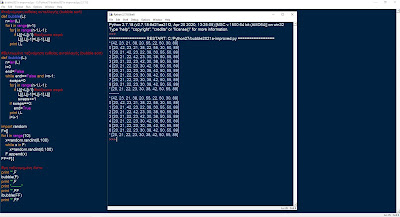
Στην Python γράφουμε μία συνάρτηση που δημιουργεί μια λίστα με την ακολουθία Fibonacci m αριθμών. Στο κυρίως πρόγραμμα ζητάμε το πλήθος m που πρέπει να είναι μεγαλύτερο του 2.

Στη συνάρτηση που παίρνει ως παράμετρο το πλήθος m των αριθμών της ακολουθίας δημιουργούμε τη λίστα με την ακολουθία. Αρχικά είναι [0,1] και κάθε νέο στοιχείο είναι το άθροισμα των δύο προηγούμενων. Αν n=len(L) τότε L.append(L[n-2]+L[n-1]). Αυτό επαναλαμβάνεται όσο ισχύει n<m ώστε να έχει η ακολουθία ακριβώς m αριθμούς.

 

 

Η συνάρτηση python και το κυρίως πρόγραμμα

Βελτιωμένος αλγόριθμος ταξινόμησης ευθείας ανταλλαγής (bubble sort) - Δημιουργία τυχαίας λίστας διαφορετικών ακέραιων αριθμών (random - randint)

 

 Ο αλγόριθμος ταξινόμησης ευθείας ανταλλαγής (bubble sort) είναι αρκετά αποδοτικός αφού δεν επαναλαμβάνει συγκρίσεις μεταξύ ήδη ταξινομημένων στοιχείων. 

Όμως, στην κανονική του μορφή, κάνει συγκεκριμένα περάσματα (n-1, όπου n το μήκος της λίστας προς ταξινόμηση), ακόμα κι όταν η λίστα είναι ήδη ταξινομημένη.

Αυτό μπορεί να διορθωθεί ελέγχοντας αν στο τέλος ενός περάσματος από τα n-1, προκύψουν μηδενικές ανταλλαγές.

Στο αρχείο python που παρατίθεται, έχουμε την απλή υλοποίηση και την βελτιωμένη. Η λίστα των αριθμών παράγεται με την χρήση της βιβλιοθήκης random και της συνάρτησης randint, ώστε να έχουμε μια τυχαία και όχι προσχεδιασμένη λίστα.    

Αρχείο Python 1

 Αρχείο Python 2

Στην εικόνα που ακολουθεί φαίνεται ο κώδικας του προγράμματος και η εκτέλεση του, όπου φαίνεται ξακάθαρα ότι σε μία τυχαία αταξινόμητη λίστα στην απλή υλοποίηση του bubble sort κάνουμε δύο περάσματα επιπλέον σε σχέση με την βελτιωμένη υλοποίηση. Σε μία λίστα 10 αριθμών η διαφορά φαίνεται μικρή, αλλά σε πολύ μεγάλες λίστες υπάρχει μεγάλη εξοικονόμηση επαναλήψεων.