Επίλυση εξίσωσης δευτέρου βαθμού της μορφής αx2 + βx + γ = 0, με α ≠ 0
με τη χρήση της διακρίνουσας Δ με Python 2.7
| Δ = β2 – 4αγ | Η εξίσωση αx2 + βx + γ = 0, α ≠ 0 |
|---|---|
| Δ > 0 | Έχει δύο ρίζες άνισες τις |
| Δ = 0 | Έχει μια διπλή ρίζα τη |
| Δ < 0 | Είναι αδύνατη στο R . |
Πηγή:
http://users.sch.gr/fergadioti1/Institude_Geogebra/applets/A_alg_3exisoseis/33.html
Στην Python δημιουργούμε μία συνάρτηση quad(a,b,c) με παραμέτρους τους συντελεστές της δευτεροβάθμιας εξίσωσης α,β και γ (a,b,c).
Πρώτα υπολογίζουμε την διακρίνουσα Δ = β2 – 4αγ (d=b**2-4*a*c)
Aν d<0 επιστρέφει το d και τα μηνύματα: "No real solution", "No real solution"
Αλλιώς αν το d>0 η συνάρτηση επιστρέφει το d και δύο ρίζες:
x1=(-b+math.sqrt(d))/(2*a)
x2=(-b-math.sqrt(d))/(2*a)
return d,x1,x2
Τέλος αν d=0 (d==0) η συνάρτηση επιστρέφει το d και μία διπλή ρίζα:
x=-b/float(2*a)
return d,x,x
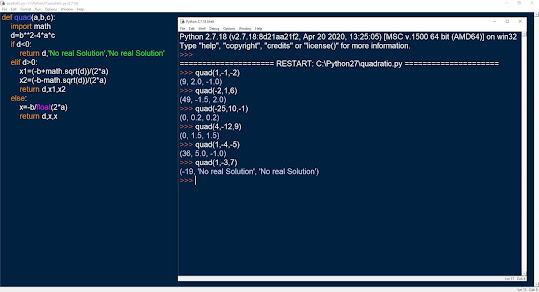
Η συνάρτηση και οι κλήσεις της συνάρτησης από τη γραμμή εντολών (εκτέλεση)
Το αρχείο Python με τη συνάρτηση επίλυσης δευτεροβάθμιας εξίσωσης